前回のあらすじ
共通テスト2014の数学の幾何学の問題（数A、数I)で、今年は星型の図形を分析する問題が出た。問題を解く前に、シミュレーターをsvg+javascriptで作ってみようと思い、プログラミングを始めた。問題の一般性を失わせずに、点A,C,P,Qをy軸に置く配置を決めたあと、自由度が２つ残る点Dをどう置くか検討し、「点Aからの距離」および「y軸からの角度」の２つの自由度を表現するプログラミングまで完成した。また、問(1)を解くために必要な点T,S,Rの設置を行い、Dの変化とともに三角形が変形できるようにし、問(1)に関連する部分が完成した。
ということで、今回はようやく高校数学に取り組むことができる....。
問(1)に取り掛かる直前に発生したバグ取り話
問題に取り組む前に、昨晩のブログ執筆の後に判明したバグの話を書いておこう。はてなブログでjavascriptが使えることがわかり、短い間隔でたくさんプログラムを調子付いて書き込んだわけだが、それぞれのブログの執筆時にプレビューで確認するときちんと機能するのに、ブログトップを表示させ、上からスクロールしてすべての記事を一斉にみていくと、全てのsvgの動きが変（でたらめ）になるという問題が見つかったのだ。
分析の結果、変数がundefinedになっていることがわかり、その原因を追求していくと、非常に当たり前の結果となって茫然自失となったのである。つまり、記事を一気に表示させると、同じ名前の変数と関数が複数回定義されてしまうのである。ブログトップで複数の記事をまとめると、全体が（htmlとして）１ページ分としてブラウザに認識されるからだ。個々の記事を１ページずつ表示するときは、変数や関数は一意的に決まるからきちんと作動する。しかし、それらをまとめた時にバグが生じるのである。
これを解決するには、各記事において変数名と関数名を変えるしかない（より緻密にはsvgのオブジェクト名も変えるのが安全）。もちろん、手動でやるのは面倒なのでsedを使って一発変換するべきなのだが、変数名がコマンド名の一部分と被っていたりして、非常に苦労した。たとえば、extend()関数がextver4end()関数になってしまったのは、xtという座標をxtver4に変更した際に、extendの２文字目と３文字目、つまりe(xt)endがe(xtver4)endに変換されてしまったからであった。こういうミスを一つ一つ解決しながら、最終的に問題ない変換公式をつくるのに、時間がかかってしまった。出来上がった時は本当に安堵した.....。hatena blogに随分負荷をかけてしまったかもしれず、申し訳ない気分でいっぱいである。
余談は以上である。では数学の問題に取り組みたいと思う。
問（１）の内容
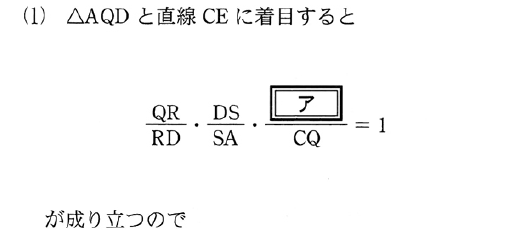
まずは最初の穴埋め問題に取り組もう。
さっそく、シミュレータ始動である！（といっても、このブログではスクリーンショットを利用する）
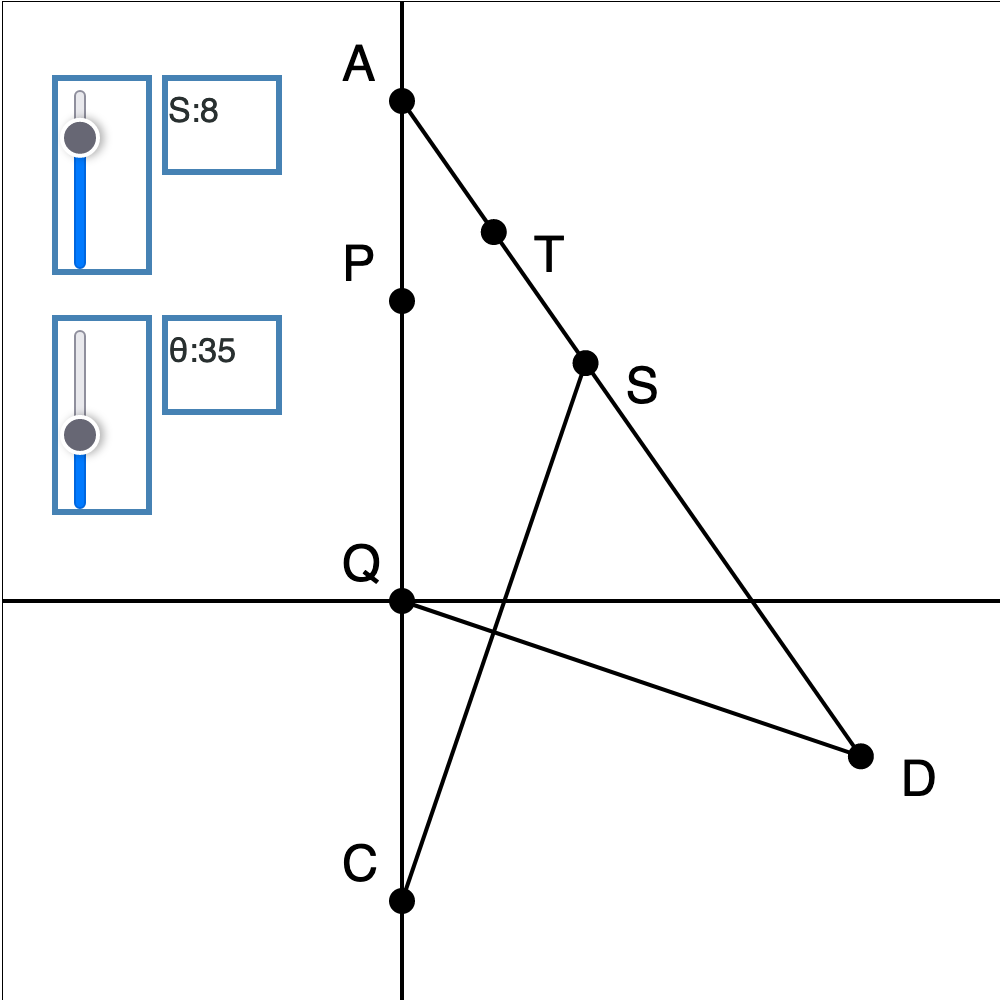点Rはシミュレータでは表示してない。というのは、連立方程式を解かねばならないからだ。この部分の実装は後でやることにしよう。点Rは線分QDと線分CSの交点である。QR/RDの値はまだ不明である。
次はDS/SAだが、こちらは問題文で与えられており、3/2である。
最後に穴埋めが出てきて、?/CQである。同じ線分のどれかが入らないと、スケーリング（S）が統一できないから、？に入るのはA,P,Q,Cのどれか二つを選んだものになるはずである。その組み合わせは$_4 C_2 = (4.3)/2 = 6$通り。CQはすでに使ってあるから５通りと言ってもいいかもしれない。デタラメに書いても1/5の確率で正解できるが、問題文の選択肢には５通り全てが列挙してあってあまり助けにならないし、ここはそういう問題じゃないのでちゃんと考えることにしよう。
標準的な手法で解くならば、どうも幾何学で教わったなんらかの定理を使うことになりそうであるが、そんなもの忘れてしまった、という場合には、パニックに陥らず、Dの自由度を生かして「代数幾何」で解けば必ずなんとかなる。
代数幾何を利用する
代数幾何はデカルトの「発明品」である。デカルト以前の数学、すなわちユークリッド幾何学の研究／勉強法というのは、一問一問がnontrivialであり、ある問題の解決法を一つ見つけても他の問題への応用度が低く、その場限りに近い感じの定理を無数に覚え、活用するというものであった（あたかも非線形方程式の特殊解の研究、たとえばアインシュタイン方程式や回転する多体問題の平行形状の分岐問題に似ている）。デカルトの代数幾何はそうではなく、「機械的に」「どんな問題」でも、誰もが解けるようにしたがすごい点である。そして代数幾何の奥義は「便利な座標系を選ぶこと」である。問題文にはいびつな形の星型が「ご親切」に掲示されているが、あのまま考えると罠にはまる。Dの自由度を使うと、もっと簡単であり、かつ一般性を失わない形の図形を手にすることができる。シミュレータをつかってみよう。
いろいろいじってわかるのは、点Dがx座標上に来た時である。またθの角度の自由度もあるので、計算しやすい、45度や60度などに限ってしまおう。ここでは45度を利用したいと思う。
直角２等辺三角形AQDに着目すれば、当然QD=AQ、かつAD=√2AQである。４点(A,P,Q,C)を組み合わせてつくった線分の比率と、３点(Q,R,D)を組み合わせて使った線分の比率が共通になった。つまり直接同じ単位で比較できる。同様に線分ADの上にある線分もは同じスケールで測れるようになった！
AQ=1とするとAP=2/5である。また、AD=√2なので、AT=√2/5、そしてAS=2√2/5である。AS = √2 APなので、三角形APSは、直角二等辺三角形である。したがって、線分PSはx軸に平行である。
となれば、三角形CPSと三角形CQRは相似な直角三角形なので、比率の計算ができる。 \begin{equation} \frac{C Q}{CP}=\frac{3/5}{6/5} == \frac{Q R}{PS} = \frac{Q R}{2/5} \end{equation} つまりQR = 1/5である。そしてRD=1-1/5=4/5である。
これにより、 \begin{equation} \frac{Q R}{RD}\cdot \frac{DS}{SA} \cdot \frac{?}{C Q} = \frac{1/5}{4/5}\cdot \frac{3}{2} \cdot\frac{?}{3/5} = \frac{?}{8/5} \end{equation} となった。線分AC上で8/5の長さを持つのは線分ACそのものである！また、すでに上の方でQR:RD=1:4という答えも出てしまった。
特殊な例１つだけでは心配、という人は、別の例を２、３やってみれば納得がいくと思う。これが一般性を保持した上での特殊化という手法のパワーである！電磁気学風にいうと「ゲージ固定」みたいなものである。ローレンツゲージの代わりに、二等辺直角三角形「ゲージ」を用いて、一般性を損なわずに問題を解き切ったのである。代数幾何というのは、こういう「機械化」「自動化」が可能なので素晴らしいのである。
点Rの座標
点Rの座標を計算し、グラフにRという記号を表示するようにプログラムを変更してみよう。 実はRは原点からのベクトル$\overrightarrow{Q R}$で書けるので意外に簡単な表現を持っているはずである。QR:RDの比率がわかっていれば、間違いなく簡単になるのはすぐにわかる。つまり \begin{equation} \overrightarrow{Q R} = \frac{1}{5}\overrightarrow{Q D} = \frac{1}{5}\left(5\boldsymbol{e}_y +r\sin\theta\boldsymbol{e}_x -r\cos\theta\boldsymbol{e}_y\right) \end{equation} となるからである。
比率がわからないときは、直線QDと直線CSの方程式を$r$と$\theta$を用いて表し、連立方程式を解いて交点の座標を求めるやり方で、上と同じ結果を得ることができる。逆に、交点の座標が上のような結果になるので、QR:RD=1:4と結論づけることも可能である。
ということで、プログラムには結果だけが必要となるので、どの方法でもよいから好みの方法で計算して上の結果を得たら、コードに組み込むだけである。その結果が以下のコードである。
