前回のあらすじ
$g(x) = xk(x), k(x)=x^2+ax+b$が与えられており、$x\rightarrow n\in\mathbb{Z}$の場合に($\mathbb{Z}$は整数の集合）、$g(n)$が素数となるかどうか($g(n)\in\mathbb{P}?$)を調べる問題をずっとやっているが、前回は、$a,b\in\mathbb{Z}$を固定した場合に、 $k(p)=1$かつ$k(-p')=-1$を満たす$p,p'\in\mathbb{P}$を4つ見つけることはできないことを証明した。ということで、考察すべき残りの状況は以下の5つとなった。
- (a) ケース3が2つの整数解を与え、ケース1とケース2が残りの２つの整数解を与えて4つとなる場合。
- (b) ケース3が２つの整数解を与え、ケース4が一つの整数解、ケース1あるいはケース2が残りの整数解を与えて４つとなる場合。
- (c) ケース3をケース4と言い換えた場合の、(a)の場合。
- (d) ケース3をケース4と言い換えた場合の、(b)の場合。
- (e) ケース1とケース2が１つずつの整数解を与え（合計２つ）、さらにケース3が一つ、ケース4が一つの解を与える場合。
本日は(a)と(b)の場合について調べてみたい。
(a)の場合とは？
ケース3というのは、$x=p\in\mathbb{P}$, かつ$k(p)=1$となる場合のことである。ただし、$\mathbb{P}$は素数の集合を表す。したがって、$g(p) = p$となるから与えられた条件を満たすというわけである。
前に数値的に探した時は、$(a,b)=(-5,7)$という具体例が一つ見つかった。この場合、$k(x)=x^2-5x+7$であるから、$k(2)=4-10+7=1$、および$k(3)=9-15+7=1$となり、$g(2)=2, g(3)=3$となって与えられた条件を満たす。
一方でケース4というのは、$x=-p'$（ただし$p'\in\mathbb{P}$）の場合に、$k(-p')=-1$となる場合のことである。この場合は、$g(-p')=(-p')(-1)=p'$となって与えられた条件を満たすというわけであるが、ケース3とケース4を同時に実現するような$(a,b)$は存在しないことを前回証明したのである。
問題を解く観点からすると蛇足に近い形になってしまうが、ケース4についても条件を満たす2つの異なる素数$p,p'$がみつかるかやってみよう。ケース4を満たすための「必要条件」、$k(-p')=-1$が$p'$についての2次方程式となり、異なる2つの正の実数解を与える条件、は \begin{equation} b < \frac{a^2}{4}-1, \quad a > 0, \quad b>-1 \end{equation} であった。下の図で紫色の影で塗られているのが該当する領域である（ちなみに緑色の影で塗られているのがケース3において2つの正の実数解を持てる条件に対応する領域）。
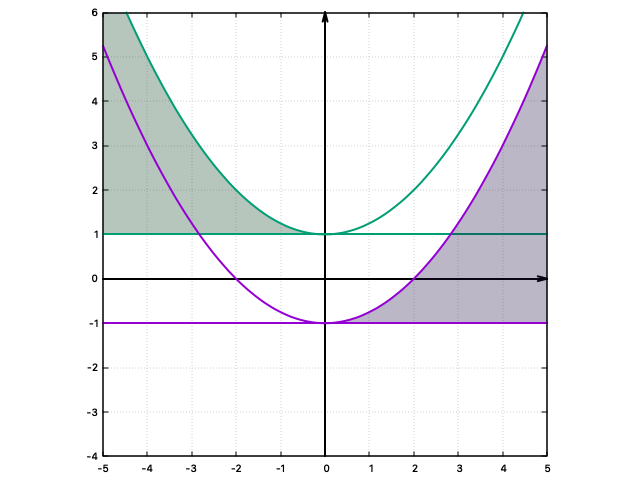
この図で確認できる格子点を探し、上の図に重ねてみる。
境界上の格子点は条件からは外さなければならない（重解となるため、解の個数が不足してしまう）が、一応計算だけはやっておくことにする。
前回作ったpythonのプログラム(discriminant.py)を再利用することができる。
まずは境界上にある格子点から計算してみる。データの見方は
通し番号, a, b, 判別式, 平方数かどうか、整数解1、整数解2
である。今考えているのはケース4なので、整数解はすべて負の整数（素数にマイナスをかけたもの）になってないといけない。
1 0 -1 0 True 0.0 0.0
2 1 -1 1 True 0.0 -1.0
3 2 -1 4 True 0.0 -2.0
4 2 0 0 True -1.0 -1.0
5 3 -1 9 True 0.0 -3.0
6 4 -1 16 True 0.0 -4.0
7 4 3 0 True -2.0 -2.0
8 5 -1 25 True 0.0 -5.0
9 Programme completed...
整数解が出ていたとしても、ケース4の場合は（絶対値が）素数でないといけないから、0.0および1.0になってしまったものを除外しないといけない。また、重解のものも外れる。ということで、予想通り境界上の格子点に条件を満たすものは存在していないことが確認できた。
次は、ちゃんと境界内部に存在する格子点（のいくつか）を確認してみよう。
1 3 1 1 True -1.0 -2.0
2 4 2 4 True -1.0 -3.0
3 5 3 9 True -1.0 -4.0
4 5 5 1 True -2.0 -3.0
5 Programme completed..
すでに説明したおおり、整数解として-1.0が含まれている場合は除外する。したがって、4行目の$(a,b)=(5,5)$が条件に該当するものであることがわかる。検算してみよう。
\begin{equation} k(-p)=p^2-5p+5 \end{equation} に対して、$k(-2)=4-10+5=-1$, また$k(-3) =9-15+5=-1$となって条件が満たされていることが確認できた。
もちろん、この解はケース3の領域に含まれていないからだめである。といっても、実数解が２つ出るところまでは大丈夫であるが、二つの正の解が出てこないという点で失敗する。確かめてみよう。
$k(p)=p^2+5p+5=1$となる$p$が素数になるかどうかである。$p$についての方程式を解くと、 \begin{equation} p = \frac{-5\pm\sqrt{25-16}}{2} = \frac{-5\pm 3}{2} = -4, -1 < 0 \end{equation} となってダメである（といっても整数解が出た部分までは「すごい」けれど、素数でもないし、正数でもないからダメはダメである）。
ケース1の場合
ケース1とは、$x\rightarrow n=1$となり、$k(1)=1+a+b$が素数になる場合である。素数になるかどうかの条件式を与えるのは面倒なので、まずは素数の必要条件である「正の数」という条件を課して、領域を狭めてみたい。$k(1)>0$であるから、 \begin{equation} b > -a -1 \end{equation} という不等式が条件に対応する。
ケース2の場合
ケース2は$x\rightarrow n=-1$となり、$k(-1) = 1-a+b$が素数に負符号をかけた値となる場合、つまり$k(-1)=-p$、ただし$p\in\mathbb{P}$の場合である。この場合も「必要条件」として$k(-1)<0$を課すことができるから、 \begin{equation} b < a-1 \end{equation} という不等式の形の条件を得ることができる。
ケース1とケース2が同時に成立すること
ケース4、あるいはケース3で見つかった$(a,b)$に対し、$k(1)$と$k(-1)$が同時に（異なる）素数となれば4つの整数解が見つかってしまい、証明は破綻する。まずは$k(1)$と$k(-1)$が同時に正数となる領域を調べてみよう。これは共通の切片$b=-1$をもつ直線グラフ（傾きは$\pm 1$)の「右側」の領域となる。正確な場所は下図の黄色で塗られた領域である。
黄色の領域は緑の領域とは絶対に共通領域を持たないことがわかる。つまり、ケース3で2つの解が見つかりつつ、ケース1とケース2で残りの２つの解が提供されることはあり得ないことが証明されたことになる。
つまり(a)の場合、4つの整数解が見つかることはないのである。
(c)の場合
（c）の場合、というのは「ケース3」を「ケース4」と言い換えた場合の(a)の場合である。この可能性はまだ否定されていない。つまり、ケース4で２つの解が見つかり、かつケース1とケース2で残りの二つの解が補充される場合である。この状況をわかりやすく領域を塗り直すと次のようになる。
紫と黄色に塗られた領域の和がそれである。
紫色の領域
この領域は閉じた領域であり、目で見て数えてしまうことが可能で、$(a,b)=(3,0), (3,1), (4,0),(4,1),(4,2)$であるが、これらの点はすでに条件を満たさないことを計算して確認済みである（境界上の点も不適であることをすでに確かめた）。つまり、可能性があるとするならば、黄色の領域に限られる。
黄色の領域
黄色の領域も、$a=5$の格子点、つまり$(a,b)=(a,b)$、ただし$b=0,1,2,3,4$、については条件を満たさないことを確認済みである（$b=5$の場合のみが条件をかろうじて満たしたが、黄色の領域の外側になってしまった）。
したがって、$a\ge 6$の格子点で、$0\le b\le a-1$を満たすものだけを調べればよい。
