前回のあらすじ
共通テスト2014の数学の幾何学の問題(数A、数I)で、今年は星型の図形を分析する問題が出た。問題を解く前に、シミュレーターをsvg+javascriptで作ってみようと思いプログラミングを始めた。そしていろいろな工夫を盛り込み、ついにシミュレーターは完成した。このシミュレータを利用しつつ高校数学に取り組んだ我々は、デカルトの方法を用いて(1)の最初と二つ目の穴埋め問題を解くことができた。さらに今回もデカルトの方法を推し進めていく。
問(1)を片付ける
QB:BDの比を求めるのが次の問題だが、星型図形の作図に成功している我々にとって、その答えはすでに自明である! \begin{equation} \overrightarrow{BD} = \overrightarrow{QD}-\overrightarrow{QB} \end{equation} であるが、 \begin{equation} \overrightarrow{Q D} = 5\overrightarrow{Q R} = r\sin\theta\boldsymbol{e}_x +\left(5-r\cos\theta\right)\boldsymbol{e}_y \end{equation} \begin{equation} \overrightarrow{QB} = -\frac{3}{5}\overrightarrow{QD}=-3\overrightarrow{Q R} \end{equation} ということはすでにわかっているので、 \begin{equation} \overrightarrow{BD}=8\overrightarrow{Q R} \end{equation} である。つまり、答えはQB:BD=3:8である。
デカルト風の「定理」の研究
「メネラウスの定理」に対抗して、なにか役に立ちそうな定理を(デカルト風のアプローチで)見つけられないか、少しだけ工夫してみた。もちろん、こういう試みがそう簡単にうまくいくわけではないことはわかっている。しかし、高校の数学でユークリッド幾何学的なものを一生懸命「習熟」させているのはちょっと(というか)かなり時代遅れではないかと思うので、あえて抵抗してみたいと思っている。
まずは以前利用した「シミュレーターの前段階」の図形を利用してみたい。
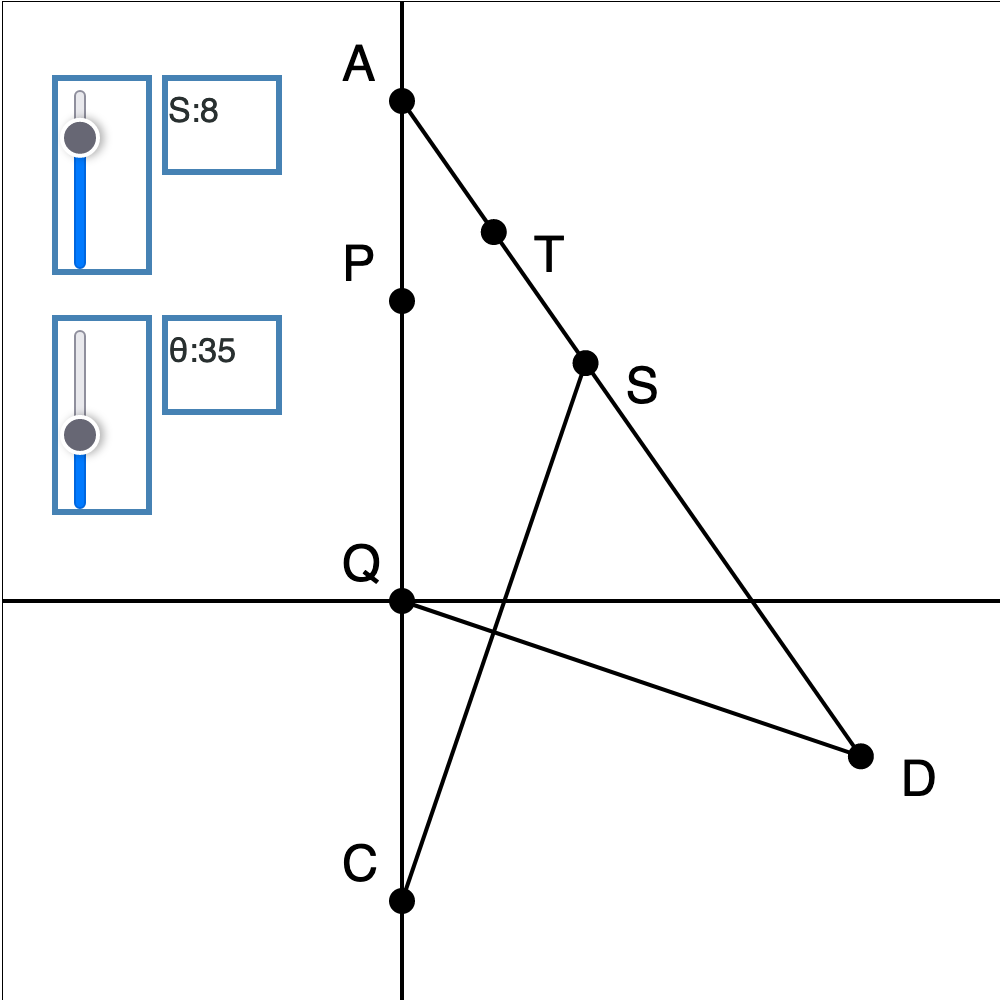
$ \triangle A C S $と$ \triangle A Q D $の面積の比に関しての関係式に着目する。両者ともに$\angle CAD $が共通なので、この角を挟む二辺$L_a,L_b$を使った有名な公式$S=\frac{1}{2}\sin\theta L_a L_b$を利用して、 \begin{equation} \frac{S(\triangle A C S)}{S(\triangle AQD) } = \frac{AC \cdot AS}{A Q \cdot AD } \end{equation} を得る。この公式自体が代数に基づく幾何によって得られるものであるので「デカルト風」のアプローチに対応していると言えるだろう。
次に、$\triangle A S C$と$\triangle CRQ$の面積比に着目する(図中でRは省略されているが、線分DQと線分CSの交点である)。再び$\angle A C S$を共通とする三角形であるから、上の有名な公式を利用して、 \begin{equation} \frac{S(\triangle CR Q )}{S(\triangle A C S)} = \frac{C Q \cdot CR}{AC \cdot CS} \end{equation} を得る。
最後は、補助線2本を利用する。両者ともに直線ADに平行な直線であるが、それぞれが点CおよびRを通過する平行線である。このとき、$\triangle A C S$と$\triangle DSR$の面積比は、底辺の比率AS:DSと高さの比率CS: RSの積によって与えられる。つまり、 \begin{equation} \frac{S(\triangle RSD )}{S(\triangle A C S)} = \frac{DS \cdot RS}{AS \cdot CS} \end{equation} である。
さて、$\triangle A C S$の面積は、$\triangle CR Q$と$\square A Q RS$の面積の和である。同様に、$\triangle A Q D$の面積も$\triangle RSD$と$\square A Q RS$の面積の和である。式の形でまとめると、 \begin{equation} S(\triangle A C S) = S(\triangle CR Q) +S(\square A Q RS) \end{equation}
\begin{equation} S(\triangle A Q D) = S(\triangle R S D) +S(\square A Q RS) \end{equation} となる。この二つの式の辺辺を引き算すると、四角形AQRSの面積を消去することができる。 \begin{equation} S(\triangle A CS)-S(\triangle A Q D) = S(\triangle CR Q) - S(\triangle R S D) \end{equation} さらに、この両辺を$S(\triangle A CS)$で割ると、 \begin{equation} 1-\frac{S(\triangle A Q D)}{S(\triangle A CS)} = \frac{S(\triangle CR Q)}{S(\triangle A CS)} - \frac{S(\triangle R S D)}{S(\triangle A CS)} \end{equation} となるが、それぞれの比は上ですでに求めてある。それを代入すると \begin{equation} 1-\left(\frac{AC\cdot AS}{A Q\cdot AD}\right)^{-1} = \frac{C Q\cdot CR}{A C\cdot CS} - \frac{DS\cdot RS}{AS\cdot CS} \end{equation} となる。ここで、AC=AQ+CQ, AD=AS + DS, CS = CR+RSを利用すると線分の種類を少なくすることができる。 \begin{equation} 1- \left(1+\frac{C Q}{A Q}\right)^{-1}\left(1+\frac{DS}{A S}\right) \nonumber \end{equation} \begin{equation} = \left(\frac{A Q}{C Q}+1\right)^{-1}\left(1+\frac{RS}{CR}\right)^{-1} - \frac{D S}{A S}\left(1+\frac{CR}{RS}\right)^{-1} \end{equation} メネラウスの定理では、AQは使わずにACが使われていて、そのおかげで「美しい関係式」が出てきた。しかしその犠牲として、線分同士の幾何学的な位置関係が「複雑」になってしまい、(多くの人にとって)記憶するのが困難な定理になっている気がする。そこで、「美しさ」をどこで導入するかという点において、ここでは「線分同士の幾何学的関係」の方に重点をおいて公式を導いてみたい。つまりは「対称性」である。
メネラウスの定理で関係する二つの重なった三角形を「キツネの頭」になぞらえる人が結構いるようなので、我々もそれに習うとしよう。まずは、キツネの「顎」として点Aを選ぶ。また耳としては点D,Cを選ぶ。つまり上図は「キツネの頭の逆立ち状態」(別名「SLIM」状態)になっているとする。
顎から耳、顎から耳、という感じで線分を左右対称に選んでみよう。そうすると、AQ/QCとAS/SDが自然な比として採用されることになるだろう。簡潔な表現にするために、この2つの比を$\alpha,\beta$と名付けよう。 \begin{equation} \frac{AQ}{QC} \equiv \alpha, \quad \frac{AS}{SD} \equiv \beta \end{equation}
次に、耳頬(S)から頭頂部(R)を経て左耳(C)にかけて線分を定義しよう。すなわち \begin{equation} \frac{SR}{RC} \equiv \gamma \end{equation} とする。
この記号を求めると、求めた式は次のようになる。 \begin{equation} 1-(1+\alpha^{-1})^{-1}(1+\beta) = (1+\alpha)^{-1}(1+\gamma)^{-1}-\frac{1}{\beta}(1+\gamma^{-1})^{-1} \end{equation}
分数の表現をなるべく無くし、多項式の形に近づけてみると \begin{equation} \alpha = (\beta+1)\gamma \end{equation} という簡単な公式が手に入った!これを狐頭の公式(ことうの公式)と呼ぶことにしよう。あるいは「複天一流の第一公式」と読んでもいいだろう(これからも新しい定理を証明する気である!)。
共通テストでは、SR:RCの代わりにQR:QDの比を求めさせているが、それを$\delta$と書いて、左右反転した狐頭の公式を書けば、 \begin{equation} \beta=(\alpha+1)\delta \end{equation} となって簡単に正解を求めることができる。
メネラウスの公式に比べれば、若干「美しさ」に欠けているが、覚えやすい幾何学的関係にあるのは確かである。また、試験問題において \begin{equation} \frac{Q R}{RD}\cdot\frac{DS}{S A}\cdot\frac{X}{C Q} =1 \end{equation} というメネラウスの公式が提示されているが、これを我々の表式に書き換えると \begin{equation} \delta \cdot \beta^{-1} \cdot\frac{X}{C Q} =1 \end{equation} となる。ここに、「複天一流の第一公式」を代入すると \begin{equation} {X}=(\alpha+1) C Q \end{equation} である。$\alpha = 5/3$であるから、$X=(8/3)C Q $である。$C Q = 3$だとすると$X=8$となるので、ACの長さに対応することがすぐにわかる。複天一流の第一の公式があれば、メネラウスの定理を知らなくても「なんとかなる」のである(というより、より記憶しやすい定理ではないかと思うのである)。