デルタ関数の定義で「規格化定数」を${1/2\pi}$にする理由は(自分なりに)納得できた。しかし、フーリエ解析で悩む学生たちは後を絶たない。
ネット検索の過程でみつけたこの「Yahoo!知恵袋」の質問でも、学生たちが苦しんでいるのがよくわかる。もちろん、回答者の説明は正しい....が、若干ポイントがずれている感じもする。質問している本人も「答えさえわかればいい」という状態に最後なってしまって、本来の質問である「どうしてデルタ関数のフーリエ変換が1になるのか教えて欲しい」という、非常に重要なポイントを忘れてしまっている感じがある。今回はおまけとして、この方の質問について考えてみたい。
「どうしてデルタ関数のフーリエ変換が1なのか?」
まずは復習
まずは、フーリエ変換の定義式を復習しよう(正確には下の式は「フーリエ逆変換」であるが)。このブログで取り上げたのは
$$ \frac{1}{\sqrt{2\pi}}\int_{-\infty}^\infty F(k)\text{e}^{ikx}dk = f(x) $$
という形である。「平面波」は「正規化」するために${1/\sqrt{2\pi}}$で割る、というルールを適用したので、本来は $$ \int_{-\infty}^\infty F(k)\frac{\text{e}^{ikx}}{\sqrt{2\pi}}dk = f(x) $$ と書くべきなのかもしれないが、最初のように書いても同じことである。
そこで、規格化因子としてではなく、フーリエ変換の「作法」として、規格化因子を”積分の前の係数”としてみなし、平面波は規格因子なしでそのまま使うという「ルール」を適用することにする....これが多くの教科書で採用されている立場である。
ただし、デルタ関数の定義式の場合だけは、「平面波」の「正規直交関係」の拡張して利用したので、規格化した平面波${\text{e}^{-ikx’}/\sqrt{2\pi} }$を${ F(k) }$として採用する。もちろん、その結果は、「デルタ関数の定義式」 $$ \frac{1}{2\pi}\int_{-\infty}^\infty \text{e}^{ik(x-x')}dk = \delta(x-x') $$ である。注:${ x'\rightarrow -x' }$としたら、${ \delta(x+x') }$の定義になるだけであるが、正規直交関係は「内積」の拡張であるから、積分に現れる2つの平面波のうち、片方は「複素共役」の形にしておく方が自然である。ということで、$\text{e}^{-ikx'}$をここでは選んでいる。
質問者の問題に近づける。
質問者の形式では$\omega$と$t$の空間の間でのフーリエ変換を考えているが、これは$k$と$x$の関係のようなものである(少なくとも相対論的な見方では)。相対論では4元ベクトル${ x^\mu=(ct, \boldsymbol{x}) }$, ${ k^\mu = (\omega/c, \boldsymbol{k}) }$を考えるからである。工学系のフーリエ変換では時間の関数として振動を分析することが多いから${ (\omega,t) }$を扱うことが多い。量子力学ではどちらも扱う。たぶん、この質問者は工学系の学生だろうと思う(純虚数を${ i }$ではなく${ j }$と書くことからも工学系であることを匂わせている)。
質問者の式に近づけるために、まずは$x'=0$とする。
$$ \frac{1}{2\pi}\int_{-\infty}^\infty \text{e}^{ikx}dk = \delta(x) $$
そして、両辺に${ \text{e}^{-ik'x} }$をかけてから、${ x }$で積分する。その際、${x}$と${k}$の積分順序を交換することは(まあ)許されるから、
$$ \int_{-\infty}^\infty dk\left( \frac{1}{2\pi}\int_{-\infty}^\infty \text{e}^{i(k-k')x} dx \right) = \int_{-\infty}^\infty \delta(x)\text{e}^{-ik'x}dx $$
となる。左辺の括弧の中は${ \delta(k-k') }$となるので、
$$ \int_{-\infty}^\infty \delta(k-k') dk = \int_{-\infty}^\infty \delta(x)\text{e}^{-ik'x}dx $$
左辺はデルタ関数の定義により1だから、 $$ \int_{-\infty}^\infty \delta(x)\text{e}^{-ik'x}dx = 1 $$ となって、質問者の最初の式、つまり「デルタ関数のフーリエ変換が1になる」にたどり着くことができた。
回答者はデルタ関数の定義
$$ \int_{-\infty}^\infty \delta(x)f(x) dx = f(0) $$
に基づいて回答している。これはこれでとても正しい。が、そもそもの質問に対する回答にはなっていない。 つまり、これだと${ f(x) }$に対するデルタ関数の性質(定義)を述べただけであって、平面波のフーリエ変換の観点からの回答にはなっていないからである。つまり、平面とデルタ関数の積の積分には2つの解釈が可能である。
平面波を関数${ f(x) }$ととらえれば、1.の解釈が成立するから回答者のような答えになる。しかし、デルタ関数を主体に考え、その「フーリエ変換」と捉えれば、回答者の答えでは「すこし的外れ」に見えてしまうのである。
デルタ関数のフーリエ変換の意味
デルタ関数も関数なのだから(厳密には超越数という関数の上の存在だが)、フーリエ変換してもいいだろう、と多くの人は考えるはずである。回答者のように考えれば、計算だけはでき、答えが1であることもわかる。しかし、これがフーリエ変換の観点から何を意味するのか考えるのはとても重要ではないだろうか?
そこで、フーリエ変換からフーリエ級数に逆戻りしてみる。フーリエ変換が1になることが意味しているのは、フーリエ級数展開の展開係数${c_n}$がすべて1になってしまうよ、ということに対応する。つまり、 $$ \sum_{n=-\infty}^\infty \text{e}^{ik_nx} \rightarrow \delta(x), \quad L\rightarrow \infty $$ という意味である。$L$は$k_n=2n\pi/L$の形で入ることは前回の議論ですでに確認した。
上の式の左辺は、ありとあらゆる周波数で振動する三角関数(波動)が同じ重み(割合)で重ね合わされるという意味である。同じ重みなので、それぞれの波の振幅はすべて1という共通の値になっていて、最大値1から最小値-1までの波がぐちゃぐちゃになって重なっている様子を思い浮かべるといいだろう。$n$の値が大きくなると、その成分の波は激しく振動する。すると異なる周波数${n'}$をもって振動する波の中で、周波数${n}$の波が激しく動き回る。そのため、その重ね合わせは「干渉」して、振幅が0になる傾向が強まる。この様子をpythonで調べてみよう。
pythonで調べる、異なる周波数をもつ三角関数の干渉
異なる周波数をもつ三角関数を同じ重みで重ね合わせたら、本当にデルタ関数になるのであろうか? 複素関数をグラフに表示するのは難しいので、ここでは${ f_n(x) = \cos(2n\pi x/L) }$を使って、その干渉$\sum_nf_n(x)$を計算し、グラフに表示してみる。偶関数を使うので和の範囲は${ n\ge 0 }$でよい。
計算では${L=1}$とし、[-0.5: 0.5]の範囲でグラフを表示する。まずは${ n=62 }$までの和(フーリエ級数の有限和、あるいは部分和と呼ばれるもの)と、${n=2}$,そして${n=40}$のグラフを同時に表示させてみた。${ x\simeq 0 }$の付近でフーリエ級数は大きな値をとるため、表示範囲を${ y\le 7 }$に制限してある。
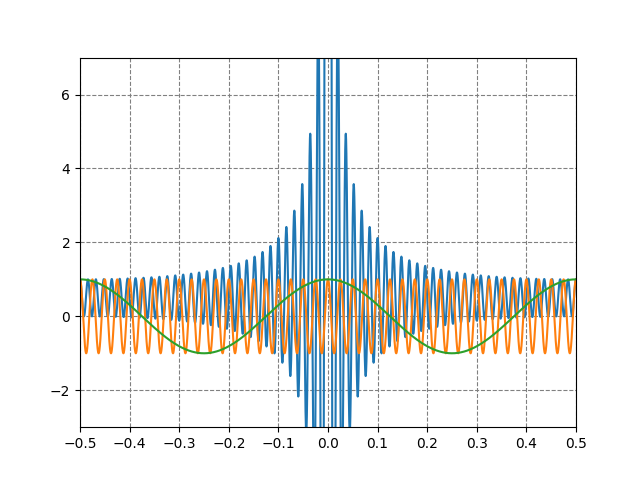
まず気がつくのは、周波数の低い(${ n=2 }$)余弦関数を縫うように、高周波${ n=40 }$の余弦関数が行ったり来たりと突き抜けている点である。両者の和を取れば、狭い範囲で高周波の正負の成分が低周波の成分に足し込まれることになる。たとえば、ある$x$の近傍を考え、わずかな変化$x+\epsilon, \epsilon \ll 1$による位相の変化を見積もってみよう。
$$ 2n\pi(x+\epsilon) = 2n\pi x + 2n\epsilon\pi $$
であるから、位相変化$\Delta\theta$は
$$ \Delta\theta = 2n\epsilon\pi $$
となる。${n}$が小さな値ならば$\Delta\theta\ll 1$となるので、低周波成分については、$f_n(x)\simeq f_n(x+\epsilon)$と近似できるだろう。一方、${ n' }$が非常に大きな場合(つまり高周波)では${ n'\epsilon }$が必ずしも小さな量に収まるとは限らない。もし大きくなったとするならば、隣の位置からわずかにずれただけでも位相はグルグル回ってしまい、ひどい場合には${ f_{n'}(x) = f_{n'}(x+\epsilon) }$となってしまうだろう。この時、各点における異なる成分の和は$f_n(x)+f_{n'}(x)$と$f_n(x+\epsilon)+f_{n'}(x+\epsilon) \simeq f_n(x) + f_{n'}(x)$となってしまうだろう。もし、$x$における和が相殺しているならば(つまり$f_n(x)+f_{n'}(x)\simeq 0$)、次の点でも同様に相殺が起きることになる。
フーリエ級数では、多様な周波数成分が無限個足されるので、ある場所$x$において、正値で寄与する成分と負値で寄与する成分はほぼ同数になるはずである。また、その振幅(絶対値)も0から1までの間の値をまんべんなくバラバラにとるだろうから、互いに相殺しあって結局は0になってしまうだろう、という予想が立てられる。
実際、${n=62}$までの部分和のグラフに、この考察に類似した状況が見え隠れしているように感じられる。ただ、まだまだ高周波部分を十分に足してないので、干渉が強め合ってしまう領域も残ってしまい、グラフはまだギザギザしている。
無限和、つまり級数が実現できれば、大抵の場所では干渉の結果、振幅が0に相殺するだろうが、どんなに高周波でも相殺しない場所が2ヶ所だけ存在する。${ x=0 }$と${ x=\pm L/2 }$である。どれほど${n}$が大きくても$x=0$を代入すると${ f_n(0)=1 }$である。したがって、部分和の項数を増やせば増やすほど、原点の干渉は強め合う。${ n=N }$までの成分の部分和ならば、その原点での値は${ N }$になる。フーリエ級数では${ N\rightarrow\infty }$だから、原点では発散することになる。
もう一つは、端点${ x=\pm L/2}$であるが、ここでは$f_n(x) = \cos(n\pi) = (-1)^n$となる。つまり、nが奇数で${-1}$、偶数で${+1}$となる。したがって、端点におけるフーリエ級数は $$ 1-1+1-1+1-1+ \cdots $$ となる。これは有名な交代級数であり、奇数の部分和では1、偶数の部分和では0となり、振動してしまう。こういうのは「発散する」と数学では定義される。しかし、原点での発散と比較すると、たとえ1であっても、それは微々たる値である。つまり、無視でき、「0」とみなしてもいいだろう。
ということで、同じ重みで三角関数を足し上げるフーリエ級数の特徴としては、原点では発散し、端点では0か1という振動値にはなるが極々小さな有限値、そしてそれ以外の点では相殺して0になる、という特徴が期待できる。この特徴はデルタ関数のそれに他ならない。
部分和を${n=101}$までに増やし、原点でのy方向の表示を100以上に設定して表示させると、次のようなグラフとなった。

収束は遅い感じがするが、確実にデルタ関数の形状に近づいているのがわかるだろう。
まとめ
デルタ関数のフーリエ変換を、その有限バージョンであるフーリエ級数に戻して考察してみた。周波数の異なる三角関数を無限個、同じ重みで足し上げると、干渉によってほとんどの場所で0に相殺する一方で、原点だけは積み上がって発散する性質がある。
実際には、デルタ関数が定義されるのはフーリエ級数ではなく、フーリエ変換である。つまり$n$が離散値ではなく、連続値、つまり実数へと拡張された場合である。端点の問題はここで解決される。$n$が実数$k$へと変更されるため、端点でも三角関数は一定値にはならず「のたうち回る」であろう。また、端点自体が$L\rightarrow\infty$の操作によって、次第に無限遠へと遠ざかっていく。このような「極限」においては、同じ重みで足し上げた(積分した)三角関数は、まさにデルタ関数となるはずである。
正弦関数にした場合
ちなみに、余弦関数ではなく、正弦関数で計算を行うと、全領域で0に収束していくかな?と思ったのだが、果たしてどうだろうか?この期待の根拠は、正弦関数では原点でも端点でも値が0になっているからである!もしこの予想が正しければ、オイラー表示で三角関数を表してフーリエ級数展開すれば、その虚数部は0に収束してくれることになる。
ところが、実際に計算を実行してみると、原点付近での収束が案外難しいことがわかった。やはり、フーリエ変換まで戻さないと厳密にはデルタ関数にはならないようである。.....というのは間違った考え方であることに、後で気がついた。下のコードを見ればわかるように、現在の計算では偶関数である余弦関数に対応して${ n\ge 0}$についての和のみを考えている。しかし、奇関数である正弦関数では負の$n$についての和も考慮しなくてはならない。ということで、虚数部は予想するまでもなく、厳密に0であった!(戒めもこめて、下のグラフは残しておく。)

pythonのコード
今回の考察に利用したpythonのコードを下に記録しておく。