前回のあらすじ
前回では、pythonを使って$\sin(x)$の数値積分を行い、計算のコツやプログラムの文法の注意点などを確認した。満足できる精度で数値積分が実行できるところまで到達したので、今回いよいよターゲットである$f(x)=\sin(x^2)$の数値積分に挑戦する。
積分のプログラム
数値積分の内容を復習しておく。次の積分である。 \begin{equation}A_k = \int _{\sqrt{k\pi}} ^{\sqrt{(k+1)\pi}} \sin ( x^2 ) dx\end{equation} この積分を、積分の台形公式を用いて、刻み幅$\delta x = (\sqrt{(k+1)\pi}-\sqrt{k\pi}) / N$、ただし$N=200$で数値計算する。$\delta x$は$k$に依存して次第に小さくなるため、$N$の値は$k$が大きいところではそれほど大きな整数にしなくても精度が保てるだろう。しかし、計算時間は大したことないので、今回は$N$は固定することにする。プログラムはその分簡潔になる。
#!/usr/local/bin/python3 # Integral of sin(x^2) # # Ver. 0 [Oct.5, 2023] import math KMAX = 400 N=200 for kc in range(KMAX + 1): xN = math.sqrt((kc+1)*math.pi) x0 = math.sqrt(kc*math.pi) dx = ( xN - x0 ) / N sum = 0.0 for i in range(N+1): x = dx * i + x0 sum += math.sin(x**2) # Edge-point handling for the trapezoidal formula sum -= 0.5*( (math.sin((x0)**2)) + (math.sin((xN)**2)) ) sum *= dx print(kc, abs(sum))
デバッグの後、$k=0, \cdots, 400$まで一気に計算してみた。グラフはgnuplotで表示。
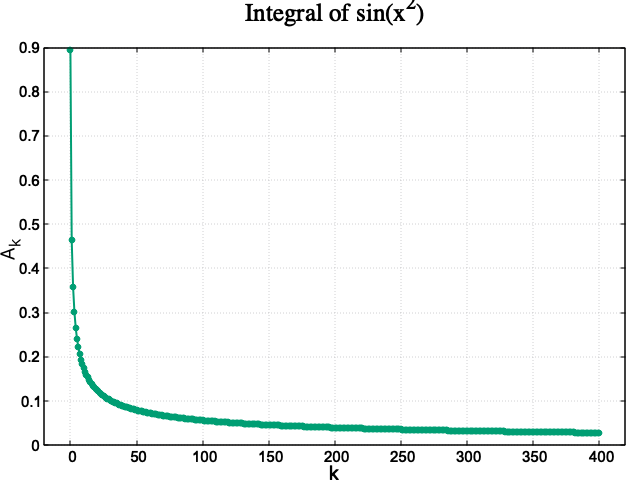
$k \sim 100$ぐらいまでは「単調減少」だとはっきり言えるが、その後、減少傾向が弱くなり、$k\simeq 400$を超えてくると、「もしかして非零値に収束?」などといった迷いが生じかねない状況が発生している。
微妙な変化を見極めるには対数グラフがいいだろう。やってみると次のようになった。
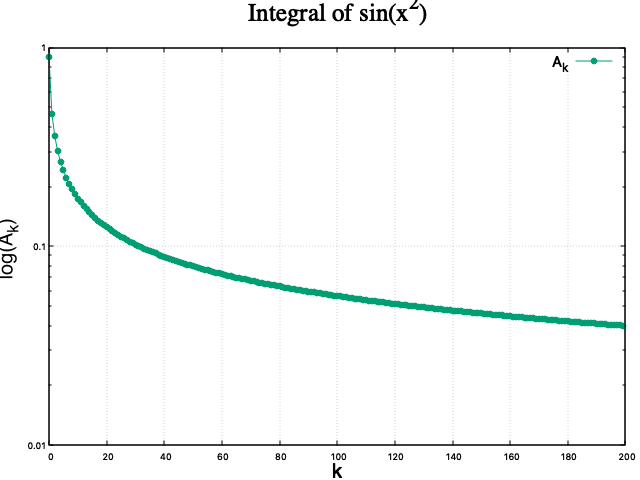
だらだらと減少し続けているように見える....。対数グラフのメモリが見やすくなるように、\begin{equation} 1-\frac{A_{k+1}}{A_k}\end{equation}を計算し、0に収束するかどうかを確かめてみる。プロットはy軸の対数グラフとした。
隣接する列の要素の比を計算する部分はawkの助けを借りた。
sinx2.py|awk 'BEGIN{n=0;v1=1.0;}{v2=$2; if(n>1){print n,1-v2/v1;} ++n; v1=v2;}' > result.dat

グラフは直線に近づきつつも、まだまだ傾きが確認できる。$k=400$程度ではまだ収束しない感じに見える。たぶん、この数列の収束はかなり「遅い」と思われる。
さて、入試の問題では積分値$A_k$が、不等式 \begin{equation} \frac{1}{\sqrt{k\pi}} > A_k > \frac{1}{\sqrt{(k+1)\pi}} \end{equation} で挟まれることを証明するのであった。もしこの不等式が成立するならば、$A_k$が単調減少列であることがいえる。 \begin{equation} \cdots > A_{k - 1} > \frac{1}{\sqrt{k\pi}}> A_k > \frac{1}{\sqrt{(k+1)\pi}} > A_{k+1} >\cdots\end{equation}
さらにこの不等式が成り立つと仮定するならば、2つの要素$A_k,A_{k + 1}$に関する不等式を組み合わせて、 \begin{equation} 0 < 1-\frac{A_{k + 1}}{A_k} < 1 - \sqrt{\frac{1}{1+\frac{2}{k}}}\end{equation}という関係式を導出することができる。 特に、不等式の右側に関しては、$k\rightarrow\infty$のとき$2/k \ll 1$であるから、テイラー展開で1次近似すると \begin{equation} 1 - \sqrt{\frac{1}{1+\frac{2}{k}}} = 1- \left(1+\frac{2}{k}\right)^{-1/2} \simeq 1 - \left(1-\frac{1}{2}\frac{2}{k}\right) = \frac{1}{k}\end{equation}となる。つまり、$k$が大きいところで \begin{equation} 1-\frac{A_{k + 1}}{A_k} \rightarrow \frac{1}{k}\end{equation} と振る舞うことが予想できる。もしそうならば、$k\rightarrow\infty$で0に収束する。
$k$が大きなところで値があまり変わらなくなる列のことをコーシー列というが、この問題の$\left\{ A_k \right\}$がコーシー列の例になっていることになる。
上のグラフに$g(x)=1/x$のグラフを重ねてみた。
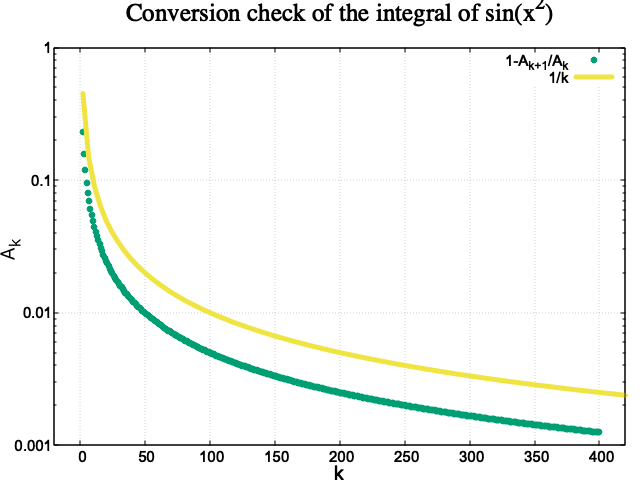
上下にずれてはいるが、$k$が大きくなった領域での振る舞いがよく似ているのが確認できる。
不等式の数値的確認
証明すべき不等式
\begin{equation} \frac{1}{\sqrt{k\pi}} > A_k > \frac{1}{\sqrt{(k+1)\pi}} \end{equation}
が実際に成立しているか、数値計算で確認して見た。
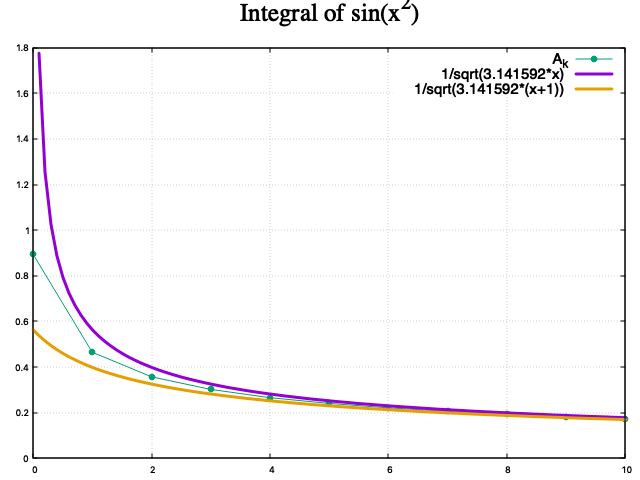
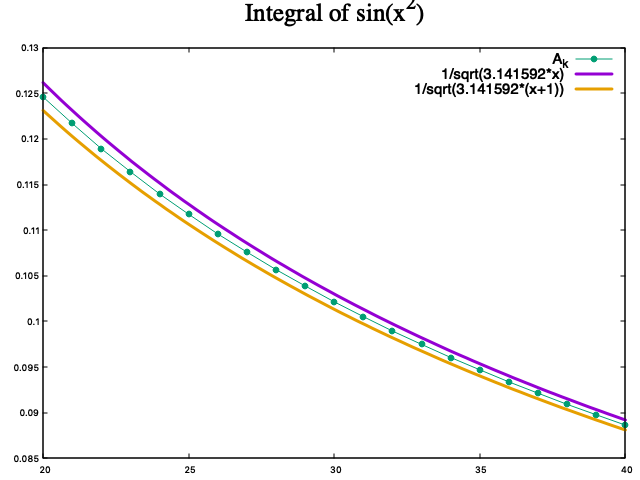
「薄皮一枚」でうまい具合にサンドイッチされているのがわかる。
数値計算で調べられるのはここまでである。どうしてこのようにうまい具合に不等式が成り立つのか、最後はやはり解析的に分析しなくてはならない。つまり試験中にやるべきこと(紙と鉛筆で数学を考えること)が、次の内容になる。
(つづく)