前回のあらすじ
この問題では放物線Bと円Cの「上下関係」を分析するように求められているが、2つの二次曲線の交点の観点から分析する手法を最初に選んだ。とはいえ、試験会場で行うような解析的な分析ではなく、コンピューターシミュレーションのようなものを利用して交点の分類を試みた。
その結果、おおよその傾向はわかり、問題に登場するパラメータ$a$(円の位置をy軸に沿って上下させるためのパラメータ)が問題の題意を満たす(単なる)必要条件としては$a >1.5$であればよい程度のことは推測できるようになった。かといって$a>1$だと題意を満たさない場合もでてきてしまうこともわかっている。我々が解くべき問題は、$a$の下限値(あるいは閾値)をどこまで下げることができるかという問題に集約されつつある。つまり$1< a_\text{min} < 1.5$という推測はできるのだが、厳密には$a_\text{min}$の値はいくつになるのであろうか?
放物線と円を直接用いたシミュレーションで分析することも可能だが、交点を用いた分析をするならば、両者に対応する方程式を連立させ、解の条件について分析することも可能であろう。それは4次方程式の根の分類に帰着できる。今回は、この4次方程式の振る舞いについてのシミュレーションを行い、答えに肉薄しようというのが目的である。
解くべき4次方程式
すでに扱うべき4次方程式は導出済みである。それは、 \begin{equation} f(x)=x^4+(1-2a)x^2+a^2-1 \end{equation} で与えられる。この方程式は、y軸に関して対称である。 \begin{equation} f(x)=f(-x) \end{equation} つまり、偶数次の項のみを含む多項式である。
パラメータ$a$を様々な値に振って、この関数の解析的な振る舞いがどのように変化するのかシミュレーションしてみよう。
今回は、pythonでグラフを作ってみる。
pythonによるグラフのプロット
以前やったpythonのプログラミングを利用したグラフ描画を、今回の題材に応用してみたい。
まずは、$a$を固定した場合を考えてみる。例えば、$a=1.5$としてみよう。描くグラフはこの$a$の値に対応した一種類である。すなわち、 \begin{equation} f_{a=1.5}(x) = x^4 -2x^2+\frac{5}{4} \end{equation} である。円Cの中心はy軸上にあり、かつその直径は2であるから、交点はかならず$|x|\le 1$の領域に発生する。したがって、グラフはこの範囲で描けば十分であるが、一応余裕を持って$x=-2$から$x=2$まで描画してみよう。グラフを描くライブラリを読み込む前に、まずは関数値の計算だけを行い、それを外部出力に送って、結果はgnuplotで表示させてみる。グラフを描くステップは$N=100$ぐらいにしておこう。
#!/usr/local/bin/python3 # Ver.0 a = 1.5 Xmin = -2 Xmax = 2 Nstep = 100 dx = (Xmax - Xmin) / Nstep for i in range(Nstep+1): x = Xmin + i * dx y = x**4 + (1-2*a)*x**2 + a**2 - 1 print(x, y)
気をつけるのは整数と浮動点小数の区別だろう。python3は浮動点小数を優先する言語なので、 4/100の結果をちゃんと0.04に「自動変換」してくれる。興味深いのは、pythonのバージョン1で 実行させると、4/100=0という結果になる点である。これは当初の設計思想ではpythonはFORTRANや C言語のように、整数の割算は整数で閉じていたようである。
また、printの書式もバージョン1と3では異なっていた。前者では括弧が不要だったようだが、後者では必須である(無いとエラーになる)。
以前の記事でも触れたが、バージョン3ではむしろ整数の範囲で割り算を閉じさせるためには注意が必要で、4 / 100が0になるようにさせるには、4 // 100と書かねばならない。
さて、このプログラムを"python"ではなく、"python3"に実行させた結果をgnuplotで描くと、次のようになった。

$a=1.5$の場合は、グラフはx軸と交点をもたず、題意を満たすことはすでに確認済みであるが、それが確認できた。
pyplotを使う
それでは、pythonのライブラリを使ってグラフを描画してみる。pyplotである。この関数はmathplotlibで定義されているので、まずはそれを読み込む。つぎに、このライブラリでは関数は配列の形で定義する必要がある。x、およびyについて2つ用意する。配列の準備の仕方は以前やった通りである。
#!/usr/local/bin/python3 #Ver.1 import matplotlib.pyplot as mpl a = 1.5 Xmin = -2 Xmax = 2 Nstep = 100 dx = (Xmin - Xmax) / Nstep x = [0.0] * (Nstep + 1) y = [0.0] * (Nstep + 1) for i in range(Nstep + 1): x[i] = Xmin + i * dx y[i] = x[i]**4 + (1 - 2*a)*x[i]**2 + a**2 - 1 mpl.plot(x,y) mpl.show()
実行すると、想像通りの結果を得ることができる。ここまでは楽勝である。

シミュレーションを始める
いよいよ本丸に入ろう。やりたいのはパラメータ$a$を様々な値に振りながら、4次関数の振る舞いがどのように変化するかを調べることである。いまのままだと、$a$の値が固定されており、一つのタイプの関数しか描画できない。さまざまな$a$の値をもつ関数を複数用意し、同時に重ねて描画するにはどうしたらよいだろうか?
一つの方法は、手で変数を複数用意することである。たとえば、$a=1.5$と$a=-1.5$の2つケースを同時に描画するときは、変数xに対し、関数y1とy2を用意しておくという手法が思いつく。
#!/usr/local/bin/python3 #Ver.1.1 import matplotlib.pyplot as mpl a1 = 1.5 a2 = -1.5 Xmin = -2 Xmax = 2 Nstep = 100 dx = (Xmin - Xmax) / Nstep x = [0.0] * (Nstep + 1) y1 = [0.0] * (Nstep + 1) y2 = [0.0] * (Nstep + 1) for i in range(Nstep + 1): x[i] = Xmin + i * dx y1[i] = x[i]**4 + (1 - 2*a1)*x[i]**2 + a1**2 - 1 y2[i] = x[i]**4 + (1 - 2*a2)*x[i]**2 + a2**2 - 1 mpl.plot(x,y1, x,y2) mpl.show()
結果は次のようになり、まあ目的は達成できる。

しかし、シミュレーションでは$a$を「振る」わけだから、たくさんの配列を用意して、異なる$a$に対応する関数を収容しなくてはならない。たとえば、$a$の可能性として50通りを想定し、そのすべてを描画したい場合、いちいち手書きで五十個の配列をプログラムに書き込むのは愚の骨頂である(プログラムというのは、そもそもこういう繰り替えし作業を人間に代わってやるのが本職である)。
一つの関数を定義するには配列が一つ必要なので、複数の関数を定義するときは配列の配列を用意すればよい。つまり、2次元配列である。pythonの場合、二次元配列はy[j][i]の形で指定でき、iの方が連続データになっているそうである。この辺りは、この解説記事を読むと勉強になると思う。
pythonで2次元配列を利用する際に苦労したのは、その宣言の仕方である。当初は
y = [[0.0] * (Nstep + 1)] * (Ndata)
とやってみたのだが、なにか様子が変であることに気がついた。どうもどの配列を見ても同じ内容になっているのである。 どうもこの宣言の仕方だと、文字通り[0.0]*(Nstep + 1)のコピーをNdata個作るだけのようなのである。それぞれが独立なNdata個の配列(その長さはNstep + 1)を設定するには、
y = [[0.0 for i in range(Nstep + 1)] for j in range(Ndata)]
とやるそうである。宣言した後、プログラム中でアクセスするときは、y[j][i]の順番となることは先に説明した通りである。
これで、Ndata種類の$a$について異なるグラフを同時に計算させることができる。 $a=-2$から$a=2$まで$\Delta a=0.04$刻みで100本のグラフを同時に計算し、重ねて描画させてみよう。 (たぶんめちゃくちゃな図になるとは思うが...。)
xの刻み幅とaの刻み幅が共通なので、まずはNstepだけを導入したプログラムを書いてみる。
#!/usr/local/bin/python3 #Ver.2 import matplotlib.pyplot as mpl amin = -2 amax = 2 Xmin = -2 Xmax = 2 Nstep = 100 da = (amax - amin) / Nstep dx = (Xmax - Xmin) / Nstep x = [0.0] * (Nstep + 1) y = [ [0.0 for i in range(Nstep + 1) ] for j in range(Nstep + 1)] for j in range(Nstep + 1): a = amin + da * j for i in range(Nstep + 1): x[i] = Xmin + dx * i y[j][i] = x[i]**4 + (1-2*a)*x[i]**2 + a**2 - 1 for j in range(Nstep + 1): mpl.plot(x,y[j]) mpl.show()
計算の結果はこのようになった。
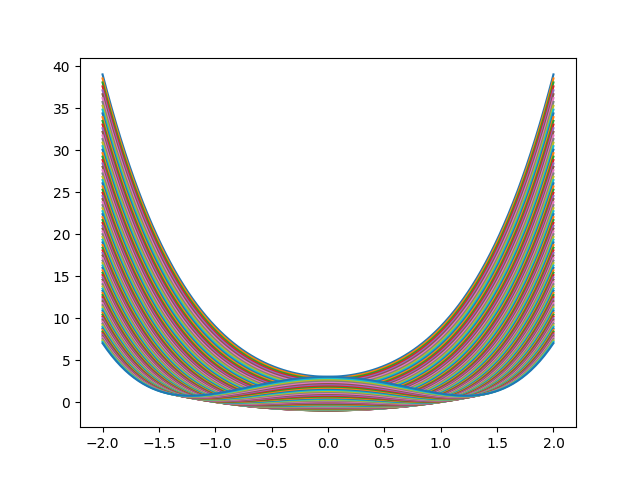
数が多すぎて水引のようになってしまった...。重ねるグラフの本数をもう少し少なくしてみる。25本に減らしてみよう。その代わり、$a$の範囲を$-2\le a \le 3$に変更して「見栄え」を気にしてみる。
#!/usr/local/bin/python3 #Ver.2.1 import matplotlib.pyplot as mpl amin = -2 amax = 3 Xmin = -2 Xmax = 2 Ndata = 25 Nstep = 100 da = (amax - amin) / Ndata dx = (Xmax - Xmin) / Nstep x = [0.0] * (Nstep + 1) y = [ [0.0 for i in range(Nstep + 1) ] for j in range(Ndata + 1)] for j in range(Ndata + 1): a = amin + da * j for i in range(Nstep + 1): x[i] = Xmin + dx * i y[j][i] = x[i]**4 + (1-2*a)*x[i]**2 + a**2 - 1 for j in range(Ndata + 1): mpl.plot(x,y[j]) mpl.show()
結果は次の通り。
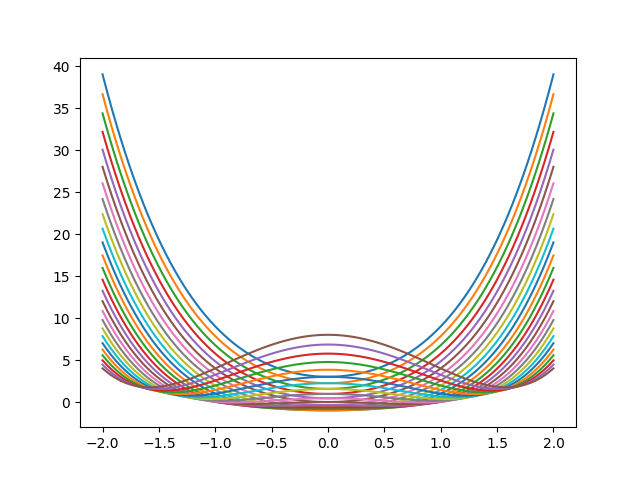
シミュレーションで分析する
このままではプログラムで遊んでいるだけ、である。あやうく、東大の数学入試問題を解いていることを忘れるところであった。4次関数のグラフがx軸と交差する場合と交差しない場合を調べるのであるから、まずはグラフに座標軸、あるいはグリッド線を描かせることにしよう。これは上のプログラムに次の一文を入れるだけで実現できる。
mpl.grid(color = "gray", linestyle="--")
グラフの拡大機能を使って$|x|\le 1$近傍の関数の振る舞いをみてみよう。

2本の茶色のグラフが$x=0$でx軸に接している状況になっているのがわかる。一つは極値が一つしかない場合であり、これは円Cが放物線Bに負の領域から接近して接した場合であることを我々はすでに分析して知っている。4次関数のy切片が0の場合に対応するので、$a^2-1=0$を解くと、その解のひとつ$a=-1$が得られる。これはBとCが接する1点で接する場合に相当していたから、つじつまがあう。一方、もう一つの解$a=1$は、(以前の我々の分析では)3点でBとCが「交差」する場合であった($x=0$に関しては接点)。
つまり、$a$が負の領域から正の領域へ増加しながら変化するとき、グラフの形は放物線のような極値を一つしか持たない形状から、次第に極値を3つ(極小1つと極大2つ)もつ形状へと変わっているのが推測できる。
最後のトドメ
ということで、試験問題の答えをシミュレーションで本気で求めようと思ったら、$a=1$から計算を初めて、$a=1.5$になるまで、細かいステップで$a$を変化させながらグラフを描く必要があることがわかる。とはいえ、最初からあまり細かくやると、また図が見にくくなってしまうので、まずは大雑把にやってみよう。25本で描いてみる($\Delta a = 1/50 $)。

この領域では、$a$の増加に伴いグラフは単純に上に「登っていく 」。したがって、一番下の水色のグラフが$a=1$の場合で、一番上の茶色のグラフが$a=1.5$の場合である。目を凝らしてみると、2本めの赤いグラフのところで、交点が初めて消失しているように見える。
拡大してみたものが下の図である。

ということで、この区間をさらに細かくみてみよう。

ということで、このシミュレーションから得た予想値$a=1.25$を使って、円Cと放物線Bを描いてみたのが次図である。

2点で接しているように見える!ということは、$a>1.25$において円Cは放物線の上に位置することが推測できる。
ということで、あとは別の方法を用いて$a>1.25$が答えであることを証明するだけとなった。 注意すべきは、1.25という数字はシミュレーションという「観測」の結果えたものであるから、有効数字の精度について吟味する必要がある。1.25=5/4であるが、この分数が厳密な答えになっているのか、それとも計算の精度を上げれば1.25からわずかながらにずれていくのか?シミュレーションではここまでが限界である。
ということで、次は(試験会場でやるべき)解析的な考察をやってみることにしよう。