前回のあらすじ
前回では「スクラッチカードシミュレーション」の結果を分析し、条件を満たす領域の境界を抜き出す作業を数値的に行なった。その結果、滑らかな曲線とおぼしき境界線が出てきた。これがどんな方程式によって作り出されているのか、今回は数値的に求めてみたい。
境界曲線の特徴
パッとみた感じは、$x=0$の頂点を持つ放物線のように見える。しかし、$(x,y)=(1,1)$の近傍で傾きが無限大、つまり垂直な直線が曲線の接線になっているように見えるので、これは放物線ではないことがわかる。放物線も、接線の傾きは原点から離れるにつれどんどん大きくなるのだが、無限大の傾きを持つのは$x=\infty$のところであって、$x=1$のような有限な位置ではない。
とはいえ、$x\simeq 0$で放物線のように「見える」のは確かである。これは原点周辺に限っていえば、放物線で近似できるという意味である。すなわち、2次のテイラー展開である。原点周りで、境界を表す曲線がテイラー展開によって \begin{equation} y = c_0 + c_2x^2 \end{equation} と表せると仮定しよう。線形項がないのは、点Aがyz平面にあることによる対称性(xの符号反転に対する系の対称性)のおかげである。角度の条件はyz平面の右と左で違いはない。
スクラッチカードシミュレーションで得た、原点近傍の数値データを2つ使うと、この2点は上の放物近似曲線を(近似の精度の範囲で)満たすから、$y_1=c_0+c_2x_1^2, y_2=c_0+c_2x_2^2$となる。これを行列を使って表すと \begin{equation} \left(\begin{array}{c} y_1 \\ y_2 \end{array}\right) =\left(\begin{array}{cc}1 & x_1^2 \\ 1 & x_2^2\end{array}\right) \left(\begin{array}{c}c_0 \\ c_2\end{array}\right) \end{equation} となる。逆行列によって係数$c_0, c_2$を求めることができる。すなわち、 \begin{equation} \left(\begin{array}{c} c_0 \\ c_2\end{array}\right) =\left(\begin{array}{cc}1 & x_1^2 \\ 1 & x_2^2\end{array}\right)^{-1} \left(\begin{array}{c} y_1 \\ y_2\end{array}\right) \end{equation} 逆行列の存在条件はその行列式が非零値をとることであるが、異なる二点であれば(Vandermonde行列式によく似た)この行列式は明らかにその条件を満たす。2x2行列の逆行列はかつては高校数学で暗記させられたものであるが、それに従えば \begin{equation} \left(\begin{array}{cc}1 & x_1^2 \\ 1 & x_2^2\end{array}\right)^{-1} =\frac{1}{(x_2^2-x_1^2)}\left(\begin{array}{cc}x_2^2 & -x_1^2 \\ -1 & 1\end{array}\right)^{-1} \end{equation}
抽出した境界線データのうち、もっとも$x=0$に近い値を持っている2つの点を選び、上の逆行列を計算してみる。
2次のテイラー展開の数値計算
スクラッチカードシミュレーションのプログラムで
Nmax = 10000
と置いた。以前計算した時はNmax=100だったので、かなり細かく計算点を取ってみた。これはテイラー展開の精度を上げるためである。計算点は細かいけれど、必要なのは二点だけなので、うまく計算を実行すればあっという間に欲しい数字が手に入る。まあ、現代のコンピュータならどんなに非力でも数分も我慢すれば全部計算してくれるとは思うが。
計算の結果次の2つの点の数値が手に入った。
x1 = 0.028317651829966893 y1 = 2.731353210515776 x2 = 0.008582817011423207 y2 = 2.731986518131477
答えを知っていれば、y1とy2が$\sqrt{3}+1$でよく近似されているのがわかるだろう。また、もちろんx1もx2も0に近い値である。
逆行列の計算は非常に単純である。
x1 = 0.028317651829966893 y1 = 2.731353210515776 x2 = 0.008582817011423207 y2 = 2.731986518131477 dt = (x2+x1)*(x2-x1) c0 = (y1*x2**2 - y2*x1**2)/dt c2 = (y2 - y1)/dt print(c1,c2)
これだけである。結果は、
c0=2.7320505813918388, c2=-0.8696596707381011
となった。この数字を用いた放物線とシミュレーションで得た境界線を、gnuplotで重ねて表示してみる。
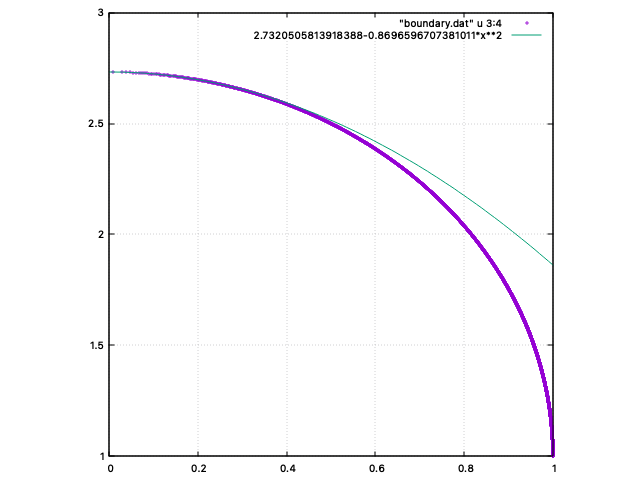
境界線を表す曲線が放物線でないとするならば、高校数学の範疇ならば、消去法で楕円か双曲線しかない(ちなみに、これらの曲線はすべて円錐曲線というグループに属する2次曲線である)。シミュレーションの結果をパッとみた感じでは、これを楕円(の一部)だと考えて、まずは解析してみるべき、と思うだろう。それで良いのである。もし、予想通りに行かなければ、その時は双曲線でやってみればよいだけのことである(双曲線でうまくいかなければ4次曲線に進めばよい!)。
楕円の方程式とテイラー展開の関係
この問題が持っている対称性により、今回考える楕円の方程式は3つのパラメータ$a,b,c$で表される。 \begin{equation} \frac{x^2}{a^2} + \frac{(y-c)^2}{b^2} =1 \end{equation}
この式を変形して$y$について解いてみると、 \begin{equation} y=b\sqrt{1-\frac{x^2}{a^2}}+c \end{equation} である。2次までのTaylor展開を行えば、上式は次のように近似できる。 \begin{equation} y\simeq b \left(1-\frac{x^2}{2a^2}\right)+c \end{equation} すなわち、先ほど計算して得た数値計算とは次の関係をもつことがわかる。 \begin{equation} c_0 = b+c, \quad c_2 = - \frac{b}{2a^2} \end{equation} $b,c$を$a$で表すと \begin{equation} b = -2c_2a^2, \quad c=c_0+2c_2a^2 \end{equation} となる。これで3つのパラメータのうち2つが消えて、残りは$a$だけとなった。
シミュレーションの結果を心眼でみる
$a$を求めるにはもう一つ条件式が必要である。これまでは$x\simeq 0$の領域で分析してきたので、$x\simeq 1$の領域を今度は利用する。ここで、シミュレーション結果をよく「みる」ことにする。すると$(x,y)=(1,1)$が境界線に乗っているように見える。 たとえ近似であっても、この性質は利用しない手はない。なんといっても、このブログの精神は「複天一流」なのである!使えるものはなんでも使うのである。
今度は近似式ではなく、厳密な楕円の方程式を利用する(実はこれには理由があるが、後述とする)。もちろん、境界曲線が楕円かどうかはまだ不明である。仮定した上で計算を進め、後でシミュレーションの結果をよく再現しているかどうかをみてから、この仮定が妥当かどうかを判断するのである。
$x\sim 1$でもテイラー展開する方が、手法の一貫性の観点から良さそうな気がする。しかし実際にやってみるとテイラー展開がうまく機能しないことがわかる。それは、この領域で境界曲線がほぼ垂直に突っ立った形状になっているからである。微分が無限大になっているという意味である。テイラー展開は微分が定義できる場所でしか利用することができない(定義からそうなっている)。そこで、楕円曲線を仮定してしまい、もしかしたら違っているかもしれないとは思いつつ、やってみてうまくいったらそのまま突破してしまおう、というアプローチを選択したのである。こういうのを「試行錯誤法」といってもいいだろう。物理学では「変分法」というタイプに属する手法である(今の問題の場合は多少複雑だが、微分ができないタイプの曲線の集合に対して変分法を当てはめた、といえるだろう)。
$(1,1)$を代入して得られる条件式は \begin{equation} \frac{1}{a^2} + \frac{(1-c)^2}{b^2}=1 \end{equation} である。ここに、テイラー展開で得られた結果を代入し$c,b$を消去すると,$a$についての2次方程式が手に入る。 \begin{equation} 4c_2(c_0+c_2-1)a^2 + (1-c_0)^2 = 0 \end{equation} 数値計算の結果は$c_0\sim 2.7, c_2\sim -0.9$であったから、$c_0+c_2-1 \sim 2.7-0.9-1 > 0$となり、$a$が実数解を持つことができることが確認できる。すなわち、 \begin{equation} a = \frac{c_0-1}{2\sqrt{-c_2(c_0+c_2-1)}} \end{equation} という形で計算できる。
数値計算の結果を用いてa2, b2, cを計算すると、
a^2 = 1.0000176119391624, b^2= 3.025338332967406, c=0.9927006071292104
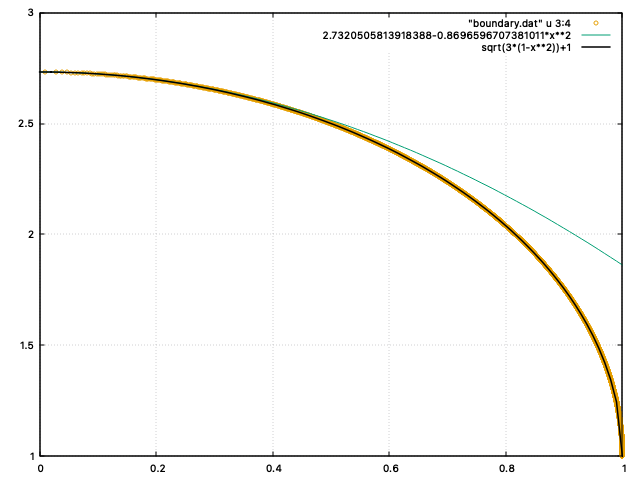
を得る。この数値結果を$a^2=1, b^2 =3, c=1$と解釈し、楕円の方程式を
\begin{equation}
x^2 + \frac{(y-1)^2}{3} =1
\end{equation}
とみなして、シミュレーションの結果と重ねて表示してみると、次のようになった。
まとめ
「心眼でみる」とか気取ったことを書いてみたが、結局は答えを知っていたから、そう書いただけにすぎない。解析的にやっても、この問題は簡単にとける(とはいえ、20分くらいはかかるだろう)。そこで楕円と直線の組み合わせになることを知ってしまえば、あとは「シミュレーションの練習」くらいなもので、簡単にここまで辿り着ける。しかし、このやり方を練習しておけば、答えがわからないときに、シミュレーションで何をすれば良いか、なんとなく察することができると思う。そのような問題はかならずこの先現れるであろう。